什么是直言命题
直言命题
直言命题是表征事物类之间的包含或不包含关系的命题,如:
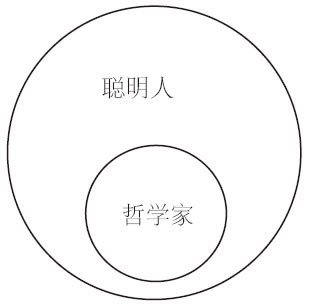
例13-1 所有哲学家都是聪明人。
例13-2 没有哲学家是聪明人。
或者类的部分之间,如:
例13-3 有些哲学家是聪明人。
或类的部分与另一个类的全部之间,如:
例13-4 有些哲学家不是聪明人。
有四种类之间的关系与直言命题相关:
一个类的全部包含在另一个类中,完全包含。
两个类完全排斥,完全不包含。
一个类的部分包含在另一个类之中,部分包含。
一个类的部分排除在另一个类的全部外延之外,部分不包含。
上述直言命题的例子中,“哲学家”是主项,“聪明人”是谓项。这些是直言命题的逻辑,而非语形(语法)主谓项。它们分别指谓一个类:每个类表达的是其元素的共仅属性。因此,“哲学家”指谓哲学家的类,“聪明人”指谓聪明人的类。
直言命题例13-1~例13-4说明了“哲学家”类与“聪明人”类之间的包含或不包含关系。这些关系可由下列方式表示:
例13-1a 所有哲学家都是聪明人。
例13-2a 没有哲学家是聪明人。

例13-3a 有些哲学家是聪明人。
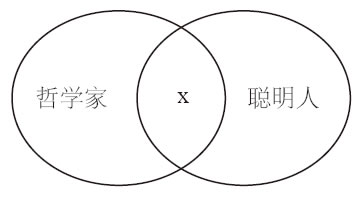
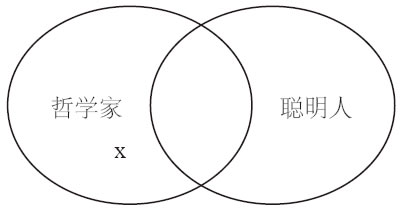
例13-4a 有些哲学家不是聪明人。
在亚里士多德(公元前384—公元前322)创建的传统逻辑中,表示直言命题逻辑形式的标准符号如下:“S”表示主项,“P”表示谓项。使用这些符号,上述直言命题的逻辑形式是:
1. 所有S都是P。
2. 没有S是P。
3. 有S是P。
4. 有S不是P。
传统逻辑中,只有具有上述逻辑形式的陈述句才是直言命题。这些命题总是表示上文提及的四种类之间的关系之一,现在,“S”和“P”代表的就是主谓项所表示类。类之间的关系参见专栏13-1。我们也可以使用圆圈图示这些关系,如图13-1所示。
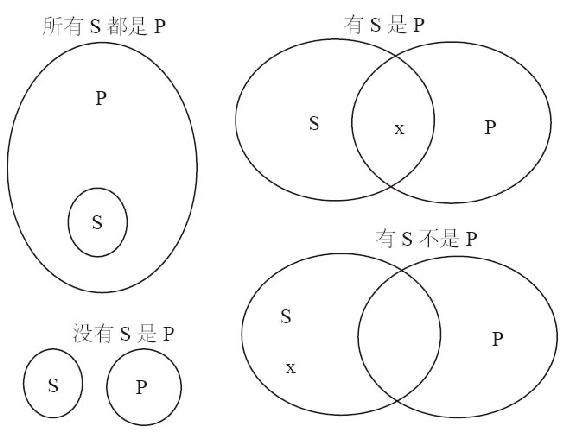
图 13-1
注意,前两个图中的“S”和“P”表示类,另两个图中的x表示S中至少有一个个体。如果“P”至少包含S的一个元素,那就等价于“有S是P”。如果S中至少有一个元素不属于P,那就等价于“有S不是P”。
专栏13-1 直言命题中类的关系
例1 表示的是 S的全部包含在P中。
例2 表示的是S和P完全排斥。
例3 表示的是部分S包含在P中。
例4 表示的是部分S排除在P之外。
标准形式
上述例13-1~例13-4是直言命题的标准形式,它们都由特定的组成部分构成。主项、谓项(不是语法上的,而是逻辑上的)当然是其组成部分。另一个组成部分是所谓的“量”:表达部分或者全部包含,或者不包含。例13-1和例13-2使用的是全称量项,“所有”和“没有”。例13-3和例13-4使用的是特称量项,“有些”。标准的直言命题还有“质”:它们是肯定形式还是否定形式,取决于是否包含否定词。例13-1和例13-3是肯定形式,例13-2和例13-4是否定形式。最后一个组成部分是或单数、或复数的系动词。以上这些就是标准直言命题的基本组成部分。
任意标准直言命题包括如下组成部分:
(1)量。
(2)质。
(3)主项和谓项。
(4)连接主谓项的联项。
任意给定直言命题,可以依据其量词种类和是否出现否定词来确定它的类型。正如表13-1所示,存在四种标准直言命题,每一个都具有独特的逻辑形式──全称肯定、全称否定、特称肯定和特称否定。

在传统逻辑中,大写字母“A”、“E”、“I”、“O”指称四类直言命题。每个字母都是一类命题的简称。这些字母是传统逻辑学家依据拉丁字母affirmo(我肯定)以及nego(我否定)发明的。每个单词的第一个元音表示全称,即“A”表示全称肯定,“E”表示全称否定;第二个元音表示特称命题,即“I”表示特称肯定,“O”表示特称否定。下文就使用字母表示四种直言命题。重新考察前文提到的例子:
例13-1 所有哲学家都是聪明人。
例13-2 没有哲学家是聪明人。
例13-3 有些哲学家是聪明人。
例13-4 有些哲学家不是聪明人。
这分别是A、E、I、O命题。
非标准直言命题
当然,很多命题都不是标准形式,也就是说,仅有一部分命题明确地包含了A、E、I、O命题中的所有组成部分。然而,通过修改可能会把许多不标准的直言命题翻译成上述标准形式之一。例如,例13-5就可以翻译为例13-5a这一A命题:
例13-5 眼镜蛇很危险。
例13-5a 所有眼镜蛇都很危险。
“每一个”、 “任何一个”、“所有事物”、“所有人”等量词都是全称的,逻辑上等价于“所有”。注意,如例13-5那样,全称量词通常会被省略。如果命题需要翻译成标准形式,那么省略的量词必须明确填写。除此之外,特定条件句也可以翻译成A命题。说所有眼镜蛇是危险的,逻辑等价于:
例13-5b 如果某物是眼镜蛇,那么就很危险。
因此,当你遇到例13-5b这类命题时,你一定要把它翻译成A命题。记住,任何看起来像全称肯定的命题,其省略的是“所有”,除非仔细解读之后是非全称的。例如,
例13-6 狗在晚上叫。
它就不能翻译为标准的A命题,只能译成I命题:
例13-6a 有些狗在晚上叫。
尽管例13-6a听起来比较怪,但我们依据的是逻辑形式:把一个命题翻译成标准形式通常都会有些奇怪。
那么,不标准的全称否定命题又是什么情况呢?如:
例13-7 我们班没有人玩纵横拼字游戏。
因为例13-7是E命题,我们可以把它翻译为标准形式,如:
例13-7a 我们班没有人玩纵横拼字游戏。
因为,一个条件句可以翻译成E命题。“我的同学中没有人玩纵横拼字游戏”等价于:
例13-7b 如果某人是我同学,那么他就不玩纵横拼字游戏。
注意,一个能够译成E命题的条件句,其后件一定包含否定词。现在考察下例:
例13-8 我同学中有人玩纵横拼字游戏。
它可以译为I命题,如:
例13-8a 我的一些同学玩纵横拼字游戏。
也可以表达为:
例13-8b 玩纵横拼字游戏而且是我同学的人存在。
也就是说,如果不包含否定词,任何关于“存在”和“有什么”的命题都可以译为I命题。如果这类命题确实包含否定词,如:
例13-9 我同学中,有的不玩纵横拼字游戏。
它可以译成“O”命题,如:
例13-9a 我的一些同学不玩纵横拼字游戏。
后面将会仔细讨论“存在预设”问题。但下一节,我们先考察与直言命题相关的推理。
直言命题的文恩图示
我们可以用标准的文恩图[由英国逻辑学家约翰·文恩(1834—1923)发明]表示四类直言命题。直言命题的文恩图采用两个相交的圆,左边的圆指谓主项表示的类,右边的圆指谓谓项表示的类。首先考察全称肯定命题的文恩图以及与之等价的一些记法。
例13-10 所有美国公民都是选民。
布尔符号:
S P=0。
A命题:
所有S都是P。
表示例13-10的文恩图由两个相交的圆构成,一个表示主项(“美国公民”),另一个表示谓项(“选民”),如图13-2所示。
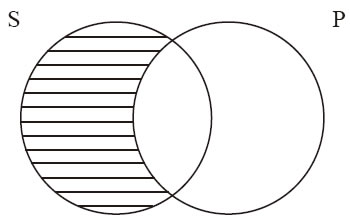
图 13-2
从例13-10可以看出,主项所指谓类的所有元素都属于谓项所指谓的类。S中的月牙部分表示没有元素(不是选民的美国公民)。文恩图中的阴影部分表示这个空间没有元素。上图中不是P的S是阴影部分,意思是,不是P的S的集合为空。这与例13-10所说的不是选民的美国公民是空类,或等价地说所有美国公民都是选民,是一致的。
上一页首先使用的是英国数学家乔治·布尔(1815—1864)发明的代数符号,“S与非P”的交集为空,然后使用传统逻辑符号,“所有S都是P”对例13-10进行了翻译。两种符号的意义可由要点中的文恩图刻画:“S与非P”的交集为空。
现考察一个全称否定命题,例13-11。
例13-11 没有美国公民是选民。如图13-3。
布尔符号:
S P=0。
E命题:
没有S是P。
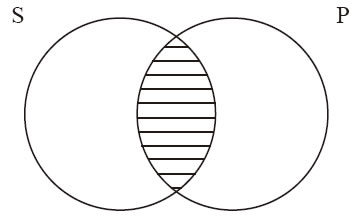
图 13-3
例13-11是全称命题,其文恩图中有一个空子类,即阴影部分:S与P相交的橄榄球形状部分表示是选民的美国公民。例13-11所刻画的是没有这样的选民:换句话说,断定例13-11意味着是选民的美国公民这个类没有元素。图的左边,例13-11的布尔表示“S P=0”告诉我们“S P”是空类。继布尔符号之后,可以找到例13-11的传统逻辑符号表示以及所属的种类。需要记住的是,对于所有全称直言命题(不管肯定的还是否定的),都存在一个表示空类的阴影部分。
接下来,考察特称肯定命题。
例13-12 有些美国公民是选民。如图13-4所示。
布尔符号:
S P≠0。
I命题:
有S是P。
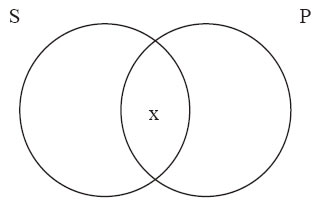
图 13-4
这次是特称命题:关于类的部分的断言。因此,上图并没有阴影,只有x,表明存在一些元素。因为“有些”在逻辑上等价于“至少有一个”,即例13-12等价于:
例13-12a 至少有一个美国公民是选民。
在中间的球形空间写上“x”,说明“S P”不是空类,而是有几个元素(至少有一个)。图上边可以看到例13-11的布尔符号翻译,“S P≠0”,即,“S P”这个子类非空,左边还有传统逻辑的符号表示。
最后是特称否定命题。
例13-13 有些美国公民不是选民。如图13-5所示。
布尔符号:
S P≠0。
O命题:
有S不是P。
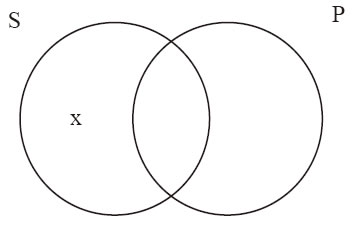
图 13-5
因为例13-13也是特称命题,所以文恩图中没有阴影。“有些”又表示至少有一个,例13-13在逻辑上等价于:
例13-13a 至少有一个美国公民不是选民。
不是选民的美国公民这个类非空,即至少有一个元素──在S与非P的交集这个子类中有x。图上边的布尔翻译指出“S与非P的交集非空”,布尔翻译之后是传统逻辑符号表示。
上述四个图可以表示四种直言命题中类的不同关系。在第14章,我们将学习如何使用文恩图检查某些三段论的有效性。但首先,让我们仔细考察任意直言命题的文恩图所表示的几个空间,如图13-6所示。
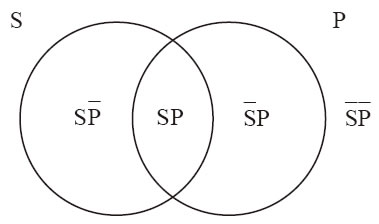
图 13-6
两个相交的圆表示直言命题中两类事物之间的关系──左边指谓的是主项的类,右边指谓的是谓项的类。两个圆所形成的空间也确定了四个子类。两圆重叠形成的中间区域为既是S又是P的元素所构成的类(同时是两个类的元素所构成的类),符号表示为“S P”。左边的月牙形表示是S但不是P的元素所构成的类,否定是通过P上面的横杠表示的。右边的月牙形表示是P但不是S的事物所构成的类,否定由S上面的横杠表示。两个圆外围的空间表示既不是S又不是P的事物所构成的类。正如我们已经看到,我们能够使用文恩图中的空间表示四类直言命题中类的包含或不包含关系。我们可以考察以“美国公民”为主项,“选民”为谓项构成的四种具体命题。这些命题所表征的美国公民和选民两个类之间的包含和不包含关系,可通过图13-7中的文恩图表示。
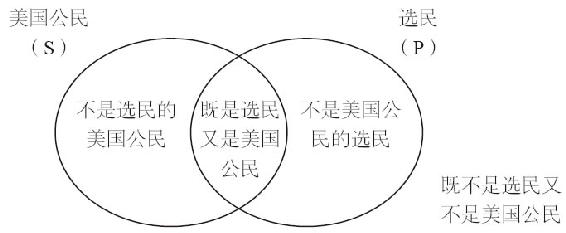
图13-7 直言命题的文恩图示
上图可以表示4个子类:(1)是选民的美国公民;(2)不是选民的美国公民;(3)不是美国公民的选民(例如,在其他国家选举的人);(4)既不是选民又不是美国公民(例如,其他国家不投票的公民,以及亨利八世、尤利乌斯·恺撒,甚至艾弗尔铁塔、大宪章、大峡谷等)。
对于每一种直言命题来说,都有一个可以说明其所涉及包含或不包含关系的文恩图。底线如下。
表征一个直言命题的文恩图可展示三个区域:相交的两个圆的内部以及两圆相交的区域。
A或E命题的文恩图包含没有元素的阴影部分。这类图中没有“x”。
I或O命题的文恩图包含一个元素为“x”的区域。这类图中没有阴影部分。
对当方阵
传统对当方阵
传统的观点是,上述4种直言命题之间的逻辑关系可以使我们进行特定的直接推理。现在学习这些包含一个前提的推理。首先来看下列传统对当方阵所表示的直接推理,如图13-8所示。
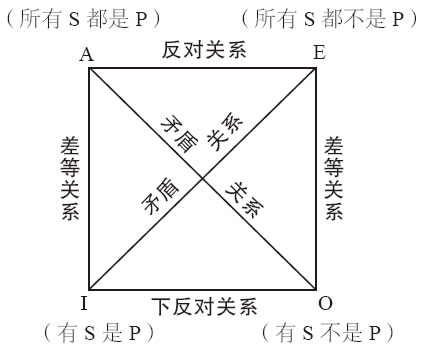
图13-8 传统对当方阵
传统对当方阵表示的是两个直言命题之间的关系,可以概括如下,如表13-2所示。
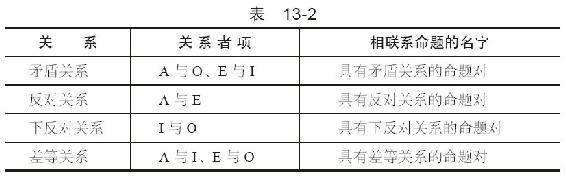
现逐一讨论这些关系。
矛盾关系 位于方阵对角线位置的两类命题构成矛盾关系。具有矛盾关系的命题不可能具有相同的真值:如果一个为真,那么另一个就为假;反之亦然。A与O,以及E与I具有相反的真值,只要两者的主谓项相同。因此,如果例13-1为真,那么例13-4为假:
例13-1 所有哲学家都是聪明人。
例13-4 有些哲学家不是聪明人。
另一方面,如果例13-1为假,那么逻辑上等价于例13-4为真。类似地,如例13-3。
例13-3 有些哲学家是聪明人。
如果例13-3是真的(至少有一位哲学家是聪明人),那么例13-2就是假的。
例13-2 所有哲学家都不是聪明人。
反过来说,如果例13-3为假,那么例13-2就为真。正如上文所述,当从一个命题的矛盾推出这个命题的真值时,就进行了一次有效的直接推理:如果它的前提为真,那么结论一定为真。但是,矛盾关系推理仅是传统逻辑学家接受的有效推理之一,还存在其他有效推理。
专栏13-2 矛盾关系

反对,下反对和差等关系 依据传统对当方阵,在特定预设下,依据下列逻辑关系的推理也是有效的:

具有反对关系的命题不能同时为真,但可以同时为假。例如,依据反对关系,如果例13-14为真,那么可以推出例13-15为假:
例13-14 所有银行家都是谨慎的投资者。
例13-15 所有银行家都不是谨慎的投资者。
这是因为这类命题不能同真,但可以同假(上述命题事实上也都是假的)。
但反对关系与下反对关系不同,两者都不同于矛盾关系。具有下反对关系的命题可以同真,但不能同假。依据下反对关系,如果例13-16假,那么例13-17真:
例13-16 有些学生是素食主义者。
例13-17 有些学生不是素食主义者。
这类直言命题不能同假,但能同真。
最后是稍微复杂的差等关系,因为真值的变化取决于是从全称到特称还是从特称到全称。逻辑上,A与同一素材的I命题是差等关系,是指:如果A命题为真,那么I命题一定为真;如果I命题为假,那么A命题一定为假。E与同一素材的O命题也具有类似关系,两者是差等关系是指:如果E命题为真,那么O命题一定为真;而且如果O命题为假,那么E一定为假。两种情况中,全称命题称为“上位式”,同质的特称命题称为“下位式”。
差等关系是以下命题之间的逻辑关系:
(1)A和I(A是上位式,I 是下位式);
(2)E和O(E是上位式,O是下位式)。
在这一关系中:
(1)真往下传递(从上位式传向下位式);
(2)假往上传递(从下位式传向上位式)。
让我们像传统逻辑学家那样依据差等关系进行推理。假设例13-18为真,那么例13-19一定为真。
例13-18 所有演奏长号的都是音乐家。
例13-19 有些演奏长号的是音乐家。
例13-18和例13-19表明,“真”往下传递。同时,因为“有些长号演奏者不是音乐家”为假,可以推出“所有长号演奏者都不是音乐家”为假──这表明“假”往上传递。但从例13-14这样的假上位式不能推出一个假下位式,因为有些银行家是谨慎的投资者是真的。
例13-14 所有银行家都是谨慎的投资者。
从例13-17这个真下位式也不能推出一个真上位式。因为,所有学生都不是素食主义者是假的:
例13-17 有些学生不是素食主义者。
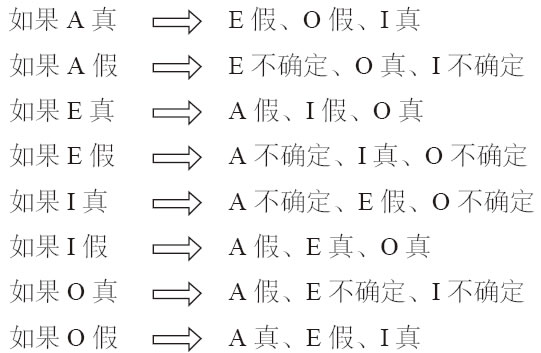
真值规则和传统对当方阵 现在,总结传统对当方阵中的所有关系,以及可以进行直接推理的规则,如下:
矛盾关系:具有矛盾关系的命题不能具有相同的真值。(如果一个为真,那么另一个一定为假;反之亦然)
反对关系:具有反对关系的命题不能同真,但可以同假。
下反对关系:具有下反对关系的命题不能同假,但可以同真。
从上位式推导下位式的差等关系(即,从全称命题推导同一素材的特称命题):
如果上位式真,那么下位式一定为真;
如果上位式假,那么下位式真值不定。
从下位式推导上位式的差等关系(即,从特称命题推导同一素材的全称命题):
如果下位式真,那么上位式真值不定;
如果下位式假,那么上位式一定为假。
已知传统对当方阵中的矛盾、反对、下反对以及差等关系,依据左边列表中假定的命题真值,我们能够推出右边列表中命题的真值。
存在预设
尽管依据反对、下反对、差等关系进行的推理被传统对当方阵断定为有效,但我们进行这类推理的能力却被全称命题和特称命题的一个有意义的差异削弱了:I和O有存在预设,A和E没有。也就是说,I和O命题含蓄地预设了它们的主项所指谓的个体存在。因为“有的”在逻辑上等价于“至少有一个”,因此形如例13-20这类命题在逻辑上等价于例13-20a:
例13-20 有些学生是素食主义者。
例13-20a 有些学生不是素食主义者。
提请注意的是,“至少有一只猫”等价于“猫存在”。类似地,形如例13-21和例13-21a这两个相互等价的O命题也预设有些猫是存在的:
例13-21 有些猫不是猫科动物。
例13-21a 至少存在一只不是猫科动物的猫。
另一方面, A与E命题逻辑上等价于条件句:例13-22等价于例13-22a,而例13-23等价于例13-23a。
例13-22 所有猫都是猫科动物。
例13-22a 如果任何事物是一只猫,那么它就是猫科动物。
例13-23 没有猫是猫科动物。
例13-23a 如果任何事物是一只猫,那么它就不是猫科动物。
以这种方式理解,一个全称的直言命题就没有存在预设,因为它等价于一个条件句,这种复合命题仅在前件为真、后件为假的情况下才为假。因此,当且仅当,一事物是猫但不是猫科动物,例13-22a才为假。而当且仅当,一事物是猫,而且是猫科动物时,例13-23a才为假。如果猫不存在,这些条件句的前件都为假,而整个条件句都是真的(无论后件是真,还是假)。
因此,反对关系推理就被削弱了:如此理解全称命题之后,当他们的主项指谓空类(没有指称)时,具有反对关系的命题就为真。考察例13-24,它与例13-24a等价。
例13-24 所有独角兽都是易受惊吓的生物。
例13-24a 如果任何事物是独角兽,那么它就是易受惊吓的生物。
因为独角兽不存在,例13-24的前件为假,整个条件句为真。现在考察与它具有反对关系的另一个命题,例13-25与例13-25a等价:
例13-25 所有独角兽都不是易受惊吓的生物。
例13-25a 如果任何事物是独角兽,那么它就不是易受惊吓的生物。
还是因为独角兽不存在,例13-25a的前件为假,整个条件句为真。显然例13-24和例13-25可以同时为真!这可以推出,除非我们假设真直言命题的主项非空,否则我们不可能推出与之反对的另一个命题为假。
那么,具有下反对关系的命题又如何呢?这涉及了I和O命题,从现代逻辑的角度看,它们确实有存在预设。尽管依据传统对当方阵,具有下反对关系的两个命题不能同假,但从现代逻辑的角度看,它们可以同假。比较例13-26与例13-26a。
例13-26 有些独角兽是易受惊吓的生物。
例13-26等价于例13-26a。
例13-26a 独角兽存在并且是易受惊吓的生物。
这样解释之后,例13-26为假,因为没有独角兽。比较例13-27与例13-27a。
例13-27 有些独角兽不是易受惊吓的生物。
例13-27等价于例13-27a。
例13-27a 独角兽存在并且它们不是易受惊吓的生物。
因为没有独角兽,所以例13-27也是假的。因此,例13-26和例13-27同时为假。这可以推出结论:依据下反对关系不可能进行有效推理。
最后是差等关系。从上文可以看出,这个关系看起来也是非常可疑的。比如说,一个人怎么可能从一个没有存在预设的全称命题推出一个具有存在预设的特称命题呢?当然,如果它们的主项指谓的事物存在,例如长号演奏者、会计以及老虎,那么从A到I以及从E到O的推理初看起来似乎没有什么问题。但涉及存在性成问题的事物时,差等关系推理可以导致谬误,例如:
例13-28 1. 所有独角兽不是易受惊吓的生物。
2. 有些独角兽不是易受惊吓的生物。
因为例13-28中的结论与上述例13-26a等价,这个论证似乎已经预设了独角兽存在!这一依据差等关系得出结论的方式失效了,因为它忽略了前提没有存在预设而结论有存在预设的事实。
现代对当方阵
上文表明,需要限制依据传统对当方阵进行的有效直言命题推理的范围。正如图13-9所示,现代方阵修改了传统方阵,消除了反对、差等以及下反对,保留了有效的矛盾关系直接推理。矛盾关系在A和O,以及E与I之间成立,它们位于方阵对角线所标出的对立的角。
从如下现代方阵可以看出,命题与其矛盾命题的否定的两点事实。第一,它们在逻辑上等价:如果位于一角的命题是真的,那么其矛盾命题的否定一定为真;而且如果它是假的,那么其矛盾命题的否定也一定为假。第二,它们互相推出:任何从一个命题到其矛盾命题的否定都是保值的,因此是有效的。
图13-9 现代对当方阵
这是依据现代对当方阵,四类标准命题之中的一个命题与其矛盾命题的否定等价(互相推出):
(1)A=非O
(2)E=非I
(3)I =非E
(4)O =非A
因此,已知(1),如果“所有橙子都是柑橘属水果”为真,那么“并非有的橙子不是柑橘属水果”为真;反之亦然。但已知(4),如果“有些橙子不是柑橘属水果”为真,那么“所有橙子都是柑橘属水果”一定为假,而“并非所有橙子都是柑橘属水果”一定是真的。读者可以尝试练习其他的有效推理。底线是对所列命题,每一对都具有相同的真值:如果一个为真,另一个一定为真;如果一个为假,另一个一定为假。前者表明有效性,两者结合就是逻辑等价。文恩图与现代对当方阵是一致的。毕竟,只有特称命题才需要“x”说明主项指谓的类有元素(如果存在)。全称命题从不要求指出有元素,只需指出没有即可(通过阴影)。
专栏13-3 逻辑等价式与有效性
逻辑等价
假设两个命题等价,若一个为真,则另一个一定为真;而且,若一个为假,则另一个一定为假。这是因为它们的真值条件相同。因此,逻辑等价的命题具有相同真值:或者同真,或者同假。所以,如果可以替换的话,其中一个可以在不改变它们所出现的复合命题真值的前提下替换另一个。例如,一个命题“P”在逻辑上等价于“并非非P”。因此,如果其中一个出现在更为复杂的表达式中,而且这个表达式又不在引号之中,那么我们就可以在保证整个表达式真值不变的前提下,用另一个替换它。
有效性
假设两个命题逻辑等价,若其中一个为真,则另一个一定为真。这就满足了“推出”或“有效性”的定义:逻辑等价的命题可以互相推出。任何由等价命题构成的论证都是有效的。
其他直接推理
现在,我们学习另外三种使用直言命题的直接推理:换位法,换质法以及换质位法。有时,换位和换质位是从全称推特称,但这类形式的有效性却需要预设全称前提中的主项非空,即不能指称美人鱼和圆的方这些空类。
换位法
换位法是通过交换“被换位命题”的主谓项位置,但不改变量和质,从而推出“换位命题”的方法。因此,E命题的换位如下。
例13-29 所有SUV都不是跑车。
例13-29a 所有跑车都不是SUV。
被换位命题的主谓项位置改变了,但其质和量保持不变,依然是全称否定。例13-29到例13-29a是有效推理:如果例13-29为真,那么例13-29a一定为真(反之亦然)。类似地,通过换位,交换被换位命题的主谓项位置之后,从一个I命题能够导出另一个换了位的I命题。例如,例13-30的换位命题是例13-30a:
例13-30 有些共和党人是记者。
例13-30a 有些记者是共和党人。
如果例13-30真,那么例13-30a一定为真,反之亦然。因此这个推理是有效的,两个命题在逻辑上等价。
然而,对于A命题,一个直接换位的推理将是无效的。因为,从例13-31显然不能推出例13-31a:
例13-31 所有猪都是哺乳动物。
例13-31a 所有哺乳动物都是猪。
但A命题可以通过“限制”换位,因为从例13-31可以推出例13-31b。
例13-31b 有些哺乳动物是猪。
限制换位中,被换位命题的量在换位命题中受到了限制:一个A命题的有效换位是I命题。其中,前者的主谓项位置进行了交换,全称量词“所有”替换为非全称量词“有的”。
最后注意,O命题没有有效换位。如果试图对真命题例13-32进行换位,那么将会得到假命题例13-32a:
例13-32 有些珍贵的石头不是翡翠。
例13-32a 有些翡翠不是珍贵的石头。
这证明了例13-32到例13-32a是无效推理。对于任意O命题,换位得到的直接推理犯了非法换位,这与从一个A命题换位得到另一个A命题所犯的谬误相同。总之,换位法的规则如表13-3所示。通过换位得到的等价式和非等价式如图13-10所示。
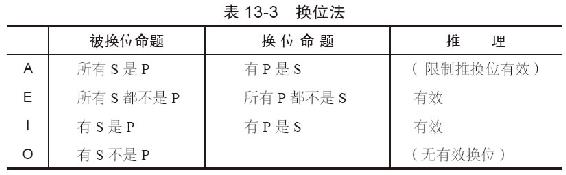
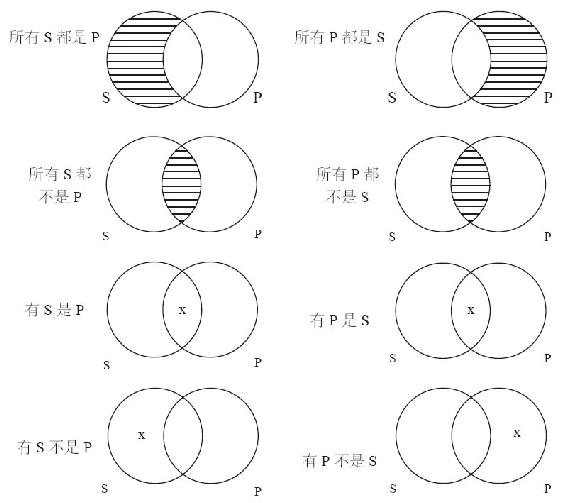
图13-10 通过换位得到的等价式和非等价式
换质法
一个直言命题的换质命题是改变它的质(即从肯定到否定,或从否定到肯定),并且在其谓项的前面增加“非”得到的。通过换质演绎出的命题称为“换质命题”,而演绎出命题的那个命题称为“被换质命题”。换质推论适用于所有命题。因此,依据换质法从例13-33这个A命题可以推出例13-33a。
例13-33 所有鹰都是鸟。
例13-33a 没有鹰是非鸟。
例13-34这个E命题换质可以产生例13-34a。
例13-34 所有手机都不是大象。
例13-34a 所有手机都不是非大象。
例13-35这个I命题的换质命题是例13-35a。
例13-35 有些加利福尼亚人是冲浪者。
例13-35a 有些加利福尼亚人不是非冲浪者。
例13-36这个O命题的换质命题是例13-36a。
例13-36 有些流行病不是灾难性的。
例13-36a 有些流行病是非灾难性的。
在上述推论中,被换质命题的谓项被其补概念所替换。例如,对于议员这个类来说,其补类是由所有非议员的事物构成的,包括市长、医生、砌砖者、飞机、蝴蝶、行星、邮票、惰性气体等。马的补类是非马,也是一个广泛而丰富的类。疾病的补类是非疾病类,如此等等。指谓任何这个补类的项称为补项。
与换位不同,四类直言命题都可以换质。对于下列四类命题,从被换质命题导出换质命题的推理都有效,如表13-4所示。通过换质得到的等价式,如图13-11所示。

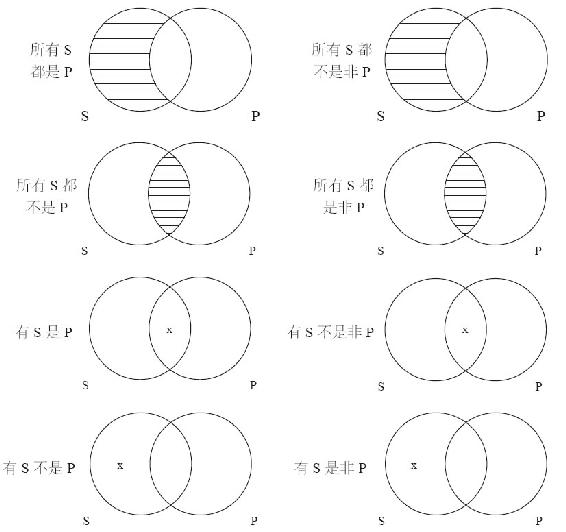
图13-11 通过换质得到的等价式
换质位法
换质位法允许我们交换一个命题主谓项的位置,并且分别在其前面添加“非”,但量和质保持不变,从而推出一个结论。因此,例13-37进行换质位可以得到例13-37a。
例13-37 所有羊角面包都是糕点。
例13-37a 所有非糕点都是非羊角面包。
使用换质位,“所有S都是P”这一A命题在逻辑上等价于“所有非P都是非S”这一A命题。两个命题逻辑等价就是具有相同的真值:如果例13-37为真,那么例13-37a就为真。而且如果例13-37为假,那么例13-37a就为假。正如专栏13-3所提到的,如果两个命题在逻辑上等价,就可以从一个推出另一个:任何这种推论都是有效的。要想形象地表示例13-37和例13-37a之间的关系,可以参看图13-12中的文恩图(可以把图中的S解释为“羊角面包”,P解释为“糕点”)。
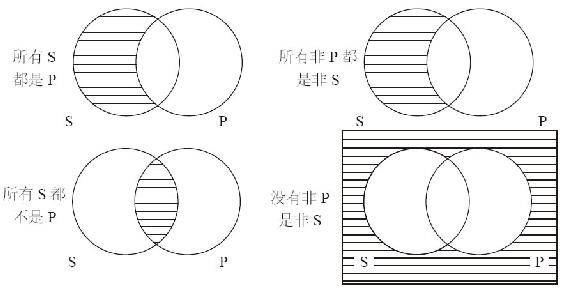
图13-12 通过换质位得到的A型等价式和E型非等价式
对I进行换质位,得到的还是量与质都相同的I命题,后者的主谓项位置与前者不同,而且前面都有“非”。例13-38的换质位命题是例13-38a:
例13-38 有些羊角面包是糕点。
例13-38a 有些非糕点都是非羊角面包。
但从图13-12中的文恩图可以看出,例13-38和例13-38a不等价。因此,任何依据换质位从例13-38到例13-38a的推论都不是有效的,犯了非法换质位谬误。
E命题也存在一个非法换质位谬误。但通过限制被换质位命题的量可以避免这个谬误。也就是说,E的有效换质位命题是O,其主谓项的位置已经被交换,而且在两个项前面都添加了“非”。因此,对例13-39进行正确的换质位(参见图13-13),限制其量、质保持不变,例13-39a是真的。
例13-39 没有美洲豹是爬行动物。
例13-39a 有些非爬行动物不是非美洲豹。

图13-13 通过换质位得到的I型不等价式和O型等价式
如果从例13-39无限制地换质位推出例13-40,那么这个推理就是无效的。
例13-40 所有美洲豹都不是爬行动物;因此,所有非爬行动物都是非美洲豹。
O命题的换质位可以产生一个等价的O命题;因此总是有效的。因此,依据换质位从例13-41可以推出例13-42。
例13-41 有些田径运动员不是跑步的。
例13-42 有些非跑步运动员不是非田径运动员。
本节内容小结,如表13-5所示。


