有效性
有时人们使用“有效的”表示“真的”或“合理的”,用“无效的”表示“假的”或“不合理的”。但是,这些与逻辑思维中的“有效的”和“无效的”意味不同。一个演绎论证是有效的,当且仅当其前提必然推出或蕴涵其结论,其中“蕴涵”的定义如专栏5-1所示。
专栏5-1 推出关系
一个论证包含推出关系,当且仅当,前提的真保证了结论的真。也就是说,如果前提全部为真,结论不可能为假。这样论证是有效的和保真的。
正如我们所见的,演绎论证的结论可以从前提必然地推出。因此,如果前提全部为真,那么结论也为真。因为一个有效论证的前提为真确保了这个结论的真,也可以说有效论证具有保真性。任何不具备保真性的论证都是一个前提为真但同时其结论为假的论证。根据定义,这样的论证是无效的:其前提没有蕴涵结论。请注意,在这里我们采用了一些不同的表述来阐明相同的概念。说论证是有效的也就是说前提蕴涵结论。而这两种说法都等同于说该论证具有保真性,即前提可以必然地推出结论。对此,我们可以总结如下:
对于一个有效论证,接受其前提但是拒绝其结论是不符合逻辑的。
一旦接受了有效论证的前提,如果你拒绝其结论(即认为它是假的),这就会是矛盾的或无意义的。矛盾的语句不可能有相同的真值:如果一个是真的,另一个一定是假的。考虑下面这个有效论证:
例5-1 如果俄亥俄河在北美,那么它不在欧洲。俄亥俄河在北美。因此,它不在欧洲。
你不能既接受“如果俄亥俄河在北美,那么它不在欧洲”和“它在北美”,但同时又拒绝“俄亥俄河不在欧洲”。这会产生矛盾,因而不符合逻辑。
有效性是用来评估演绎论证的一个标准。论证是否有效从来不是程度问题,要么完全有效,要么根本无效。论证不可能在“某种程度上有效”。它要么是有效的,要么不是有效的。此外,确定论证的有效性有一个简单的测试。当你分析一个论证时,问自己:“所有前提为真但是结论为假可能吗?”如果是,论证没有通过测试:它是无效的。相反,如果不是,你可以认为它是有效的。我们来考虑一些例子。假设我们尝试预测在巴尔的摩,下一个夏天将会是什么样的。我们也许会说:
例5-2 下一个夏天的巴尔的摩,有几天会很热。毕竟,根据巴尔的摩的过去一百年的记录,几乎所有的夏天有几天都很热。
或者想象我们对欧洲假期的期望。我们也许会说:
例5-3 伊夫是巴黎人并且讲法语。奥黛特、马蒂尔德、玛丽、莫里斯、吉勒斯、皮埃尔、雅克和吉恩?刘易斯同样如此。因此,所有巴黎人都讲法语。
很明显,即使前提为真,这两个论证的结论也可能为假。虽然这样的可能性似乎不大,但它仍然是可能的。因此,这两个论证是无效的。在声称假结论是“可能的”时,我们考虑的是逻辑可能性。在这里,讨论的重点并不在我们现实世界中,对于例5-2和例5-3,是否可能前提为真但结论为假。相反,如果存在某个可能的场景(即没有内部矛盾的场景),使得这些论证的前提为真同时结论为假,那么这些论证就是无效的。
同时,我们还要注意另一件事情:论证是否有效完全是一个结论是否可以从前提必然推出的问题。前提和结论各自的“实际”真或假,与论证的有效性基本无关。重要的是,是否前提为真但同时结论为假,因为这可以确定论证的无效性。因此,有效论证能有一个或更多假前提,但有一个真结论。例如:
例5-4 1. 所有狗都是鱼。
2. 所有鱼都是哺乳动物。
3. 所有狗都是哺乳动物。
在某些情况下,一个有效论证可能完全由假语句构成,如:
例5-5 1. 所有民主党人都是素食主义者。
2.所有素食主义者都是共和党人。
3. 所有民主党人都是共和党人。
因此,最好把有效性看作论证的前提和结论之间的一种关系,其中构成论证的语句的“实际真或假”基本上是不相干的。最关键的是:由前提真是否必然得出结论真?如果是,论证就是有效的。否则,论证是无效的。
专栏5-2 有效论证与无效论证
(1)论证可以分成两类:有效的和无效的。
(2)只有有效论证是保真的:如果它们的前提为真,则它们的结论不可能为假。
(3)只有有效论证的前提才蕴涵结论。
(4)一个接受有效论证前提的逻辑思考者不可能在没有矛盾的情况下拒绝其结论。但这种情况不会在无效论证中发生。
有效论证和论证形式
论证的形式是每个论证例示的逻辑模式。同一种论证形式通常是许多实际论证的底层模式。要表示论证的形式,最常用的方法是用占位标注或符号(如大写字母)替代某些词,而只保留具有逻辑功能的词。例如,对于例5-4,我们可以用“A”替换“狗”,“B” 替换“鱼”,“C”替换“哺乳动物”。所得到的论证形式是:
例5-4a 1. 所有A都是B
2. 所有B都是C
3. 所有A都是C
例5-4a是一个有效的论证形式,因为任何具有这种逻辑形式的论证都是有效的:如果前提为真,那么结论必定为真。上述例5-5以及下面这个例子也可以例示此形式:
例5-6 1. 所有笔记本电脑都是计算机。
2. 所有计算机都是电子设备。
3. 所有笔记本电脑都是电子设备。
因为上述例5-4同样例示了论证形式例5-4a,且该形式是有效的,因此例5-4是有效的,这与其前提是假的并不相关。对于一个有效的论证,可以具有下列情况:所有前提均为假,如例5-4;一个假结论和至少一个假前提,如例5-7;甚至所有前提和结论都为假,如例5-5。
例5-7 1. 所有专业足球运动员是运动员。
2. 所有运动员是大学生。
3. 所有专业足球运动员是大学生。
因为这些论证都例示了一个有效的论证形式,所以它们都是有效的。它们的形式使得用真前提例示它们的任何论证都必定有一个真结论。
有效性和论证形式
在例示一种有效形式的任何论证中,前提和结论之间有一种蕴涵关系。如果论证的前提为真,那么它的结论不可能为假。有效性就是这种关系。在一个论证中,可能有一个或更多的假前提,但这一事实对于它的有效性并不重要。有效性完全只与论证的形式有关。
无效性也是论证形式的问题:一个论证形式是无效的,当且仅当该论证的形式可能有真前提和假结论。但是这里的“可能”是“逻辑上可能”,也就是说无效论证也可能有真前提和真结论。例如:
专栏5-3 无效性和反例
证明某个论证无效的反例是另一个例示相同形式但是有真前提和假结论的论证。
要找到一个反例,可能需要想象一个没有内部矛盾的“可能”场景。现实世界只是众多被称为“可能世界”的可能场景中的一个。
例5-8 1. 所有的宝马都是机动车。
2. 有些摩托车是机动车。
3. 有些摩托车是宝马。
例5-8的结论是真的(的确,三个语句都是真的),但该论证是无效的,因为它例示了一个无效的论证形式,即
例5-8a 1. 所有A都是B
2.某C是B
3. 某C是A
任何例示此类论证形式的论证都没有蕴涵关系,因为结论不能必然地从前提得出。要证明一个论证是无效的,逻辑思考者用反例的方法:他们尝试想出一个论证形式完全相同但却具有真前提和假结论的论证。例如,下面这个论证是证明例5-8a无效性的一个反例:
例5-9 1. 所有煎锅都是炊具。
2. 有些饼干模具是炊具。
3. 有些饼干模具是煎锅。
例5-9跟例5-8的形式完全相同,但是有真前提和假结论。反例方法不仅可以用来证明某类论证形式的无效性,也可以用来证明具有这些形式的实际论证的无效性。因此例5-9是例5-8的一个反例。也就是说,例5-9是证明例5-8的无效性的一个例子,因为它表明了一个形式完全相同但是具有真前提和假结论的论证是可能存在的。换句话说,例5-8的真前提并不会必然推出真结论。
作为术语的“有效性”
上面我们使用了“有效”和“无效”,但是不存在“有效的语句”和“无效的语句”。尽管我们在日常语言中会听到这样的表述,但是“有效”和“无效”是逻辑术语,不能用在单个语句上,而只能用在语句间的关系上(即称为论证的关系)。“有效”只能用在一个前提必然推出结论的论证上,“无效”只能用在那些前提不能必然推出结论的论证上。只有语句间的某些关系才有可能是有效的或无效的。因此,这些术语只能用在论证上,而不能用在单个语句上。
现在,要注意另一点:因为有效性的要求非常高,所以一些被这个标准判作无效的论证可能在一个要求不怎么高的条件下有其他价值。结论不能从前提必然得出的一些论证也是可以通过概率进行推导的。换句话说,对于有些论证,前提真未必能保证结论真,但结论真仍然是可能的。在许多情况下(例如,当它们支持关于自然或者人类社会的一般机制时),这类论证对我们可能非常有用。让我们回想一下“归纳”论证:虽然它们的前提可以给结论提供一些理由,但却绝不蕴涵结论。根据这个定义,所有归纳论证都不能达到有效性的标准。但是有一类论证,即使它的前提并不蕴涵结论,却因前提能为结论提供很强的支持理由,从而使人们相信它。我们将在第6章具体讨论这类论证。
同时,说一个论证是“真的”或者“假的”也是无意义的。“语句”和“信念”可能为真或为假,但是论证没有真值!与“有效性”和“无效性”类似,“真”和“假”也是术语,不能与日常的用法混淆。记住,在逻辑思维中,
语句:
要么是真的,要么是假的;
但既不是有效的,也不是无效的。
论证:
既不是真的,也不是假的;
但要么是有效的,要么是无效的。
命题逻辑中的论证形式
如我们所见到的,说论证有效的另一个方法是论证保真性。也就是说,如果论证的前提为真,则结论必须为真,即前提的真保证结论的真。保真性是有效论证所例示的形式具有的一个特征。有些论证具有保真的特质,因为组成其前提和结论的语句的组合方式形成了一种特殊的关系,从而将前提的真(如果前提为真)传递给论证的结论。还有些论证也具有保真性,因为在组成其前提和结论的语句中有一些通常被称为“项”的表达式,它们之间有某种特定的关系,从而使得论证的结论在前提为真的条件下也为真。前一种论证是“命题的”,后一种是“直言的”。
稍后我们将对两种论证分别进行分析。但在这之前,我们必须明确我们所说的“命题”到底是什么。我们已经知道,命题是一个信念或语句的“内容”,具有真值:要么为真,要么为假。现在我们来看一些命题论证。对于这些论证,保真性取决于组成论证的前提和结论的语句间的组合关系:
例5-10 1. 如果我的手机在响,那么有人正在给我打电话。
2. 我的手机在响。
3.有人正在给我打电话。
根据例5-10的各个命题之间的关系,它是一个有效的论证。前提1由两个简单命题通过“如果……那么……”连接起来,前提2断言了两个简单命题中的第一个。用大写字母作为代替每个简单命题的符号,保留逻辑联结词“如果……那么……”,例5-l0的论证形式就很清楚了:
例5-10a 1.如果M,那么C
2. M
3. C
例5-10a的M代表“我的手机在响”,C代表“有人正在给我打电话”。例5-10a不是一个论证,而是表示论证前提和结论间关系的一个论证形式。通常称之为“肯定前件式”。任何具有这种形式的论证都例示了一个肯定前件式。例如:
例5-11 1. 如果必须有脑才能思考,那么无脑生物就不能思考。
2. 有脑才能思考。
3. 无脑生物不能思考。
下面来看另一种命题论证形式──“否定后件式”。
例5-12 1. 如果经济有增长,那么经济正在复苏。
2. 但是经济没有复苏。
3. 所以经济没有增长。
用符号记作:
例5-12a 1. 如果G,那么E
2. 并非E
3. 并非G
专栏5-4列出了一些有效的命题论证形式。现在我们对其中的部分形式进行实例分析,其他的形式将在第12章继续分析。
例5-13 1. 如果内陆温度升高,那么农作物会受到损害。
2. 如果农作物受到损害,那么我们都会遭受损失。
3. 如果内陆温度升高,那么我们都会遭受损失。
专栏5-4 一些有效的命题论证形式
肯定前件否定后件 如果P,那么Q如果P,那么Q P并非Q Q并非P 假言三段论析取三段论(1) 如果P,那么Q或者P或者 Q 如果Q,那么R并非P 如果 P,那么RQ 换质位析取三段论(2) 如果 P,那么Q或者 P 或者Q 如果并非 Q,那么并非 P并非QP例5-13是假言三段论的一个例子,因为它有如下所示的形式:
例5-13a 1. 如果 I,那么 C。
2. 如果 C,那么 A。
3. 如果 I,那么 A。
同样,你可以自己证明下面的例5-14和 例5-15是专栏5-4“析取三段论”的两个例子,例5-16是“换质位”的例子:
例5-14 1. 美国的丹尼斯?蒂托或南非的马克?沙特尔沃思是第一个太空游客。
2. 南非的马克?沙特尔沃思不是首位太空游客。
3. 美国的丹尼斯?蒂托是首位太空游客。
例5-15 1. 美国的丹尼斯?蒂托或者南非的马克?沙特尔沃思是第一个太空游客。
2. 美国的丹尼斯?蒂托是不是首位太空游客。
3. 南非的马克?沙特尔沃思是首位太空游客。
例5-16 1. 如果波斯是一个强大的王国,那么莉迪亚是一个强大的王国。
2. 如果莉迪亚不是一个强大的王国,那么波斯不是一个强大的王国。
所有这些论证都是专栏5-4中的某个论证形式的替换实例,并且都是有效的。也就是说,任何具有其中某个形式的论证都有一个推出关系,无论符号代表的实际语句是什么。换句话说,例示专栏5-4中的形式的论证都不可能同时具有真前提和假结论。这类形式的论证有很多,但是我们要在第12章对它们进行更深入地分析。
建议:本小节有很多有效的论证形式,可以制作一张卡片,以便参看和熟悉。卡片的一面是命题论证的形式,另一面是直言论证的形式。
直言论证的形式
很多论证显然是有效的,即使它们不符合命题逻辑的任何形式。例如:
例5-17 1. 所有牙医都有整洁的牙齿。
2. 常医生是一位牙医。
3. 常医生有整洁的牙齿。
例5-17显然是有效的,因为如果前提为真,那么结论必定也为真。现在我们用命题逻辑中的论证形式把每个部分替换成字母符号,就可以得到下面的形式:
例5-17a 1. D
2. C
3. E
但是例5-17a是一个无效的形式,因为有反例:即同种形式的、具有真前提和假结论的论证。如:
例5-18 1.鲸鱼是哺乳动物。
2. 加利福尼亚是美国人口最多的州。
3. 地球是平的。
因此,用一个无效的论证形式(如例5-17a)来表达一个有效的论证(如例5-17),是错误的。我们需要一个不同的形式系统,其中的字母符号不代表命题。也就是说,例5-17a的形式化太过笼统,不能作为例5-17的正确的论证形式。因为例5-17中的推出关系取决于组成论证的“命题”的各个表达式之间的关系,而不是取决于组成前提和结论的各个命题本身之间的关系。例5-17中的推出关系取决于诸如“所有”、“常医生”、“牙医”以及“整洁的牙齿”之类的项之间的关系。
形如例5-17的论证需要一个更细化的形式化表达。我们采用下列规则:
(1)将“to be”(“是”)的现在时作为每个前提和结论的主句动词。
(2)明确表达任何逻辑表达式,诸如“所有”“有些”、“没有”。
(3)用大写字母替换如“牙医”、“整洁的牙齿”之类的表达式。
(4)用小写字母替换表示特殊事物或个人的表达式,如“常医生”、“菲多”、“我”、“那张椅子”。
用这样的规则,我们就可以知道例5-17的逻辑形式与例5-19类似:
例5-19 1. 所有生产苏打饮料的企业生意都很好。
2. 百事是一个生产苏打饮料的企业。
3. 百事的生意很好。
例5-19的论证形式是:
例5-19a 1. 所有A都是B。
2. c是A。
3. c是B。
例5-19a中的“A”代表“生产苏打饮料的企业”,“B”代表“生意很好”,“c”代表“百事”。我们也可以用这样的规则对下面这个论证进行形式化:
例5-20 1. 所有眼科医师都是医生。
2. 有些眼科医师很矮。
3. 有些医生很矮。
例5-20无疑是一个有效的论证:它是直言论证的一个有效形式的替换实例。
再看一个相同形式的例子:
例5-21 1. 所有红松鼠都是啮齿动物。
2. 有些红松鼠是野生动物。
3. 有些啮齿动物是野生动物。
例5-20和 例5-21的都有如下形式:
例5-20a 1. 所有A都是B。
2. 有些A是C。
3. 有些B是C。
这里的“A”代表“红松鼠” (或“眼科医师”),“B”代表“啮齿动物” (或“医生”),“C”代表“野生动物”(或“很矮”)。
现在让我们回忆本节开始提到的一点:判断有效性的另一个方法就是确定一个论证是否具有一个有效的形式。
考虑下面这个论证:
例5-22 1. 没有伯罗奔尼撒人是埃维厄人。
2. 所有斯巴达人都是伯罗奔尼撒人。
3. 没有斯巴达人是埃维厄人。
即使一点都不懂希腊地理的人也能看出这个论证是有效的,因为它是专栏5-5中第三个有效形式的一个实例。没有一个具有这种形式的论证同时具有真前提和假结论。类似地,论证例5-23是有效的,即使前提为假。为什么?就因为它是专栏5-5中的第三个有效形式的实例。
专栏5-5 一些有效的直言论证形式
12 所有A都是B有些A是B 没有B是C所有A都是C 没有C是A有些C是B 34 没有A是B所有A都是B 所有C都是A所有C都是A 没有C是B所有C都是B 56 所有A都是B所有A都是B 所有B都是C有些A不是C 所有A都是C有些B不是C例5-23 1. 所有苹果都是橙子。
2. 所有香蕉都是苹果。
3. 所有香蕉都是橙子。
那么,有效性就完全是论证形式的问题。上述这些例子的有效性也都是形式的问题。因此,我们可以得出另一个要点:对于每一个有效的形式,所有具有该形式的论证都是有效的。同样,对于每一个无效的形式,任何具有该形式的论证都是无效的。
命题的还是直言的
当你看到命题之间的某些连词,如“或者……或者……”以及“如果……那么……”,最好按命题逻辑的形式重构论证。
另一方面,如果你看到前提中有某些表示数量的词,如“所有”、“没有”、“有些”,最好按直言论证的形式重构论证。
有效性的实际作用
逻辑思考是有目的的,如学习、理解或者解决问题。每一种目的都要求论证分析,有时还需要驳斥论证,即证明一个论证无效的过程。但是,驳斥完全不是逻辑思考的主要目的之一,而只是在某些情况下论证分析过程中不可避免出现的结果。实现逻辑思考的主要目的在很大程度上取决于对论证的宽容地、忠实地重构。对于演绎论证,宽容原则要求使得论证尽可能有说服力,最大化前提和结论的真以及论证形式的有效性;而忠实原则要求尽量捕捉论辩者的意图。在所有这些过程中,逻辑思考者努力获取论证的正确形式,补充隐含的前提(如果需要的话)。论证一旦被重构,我们就可以对其进行评估。请记住下面的规则:
不要仅仅根据一个论证的结论批判或接受一个论证。
对论证的形式或者某个明确可辨认的前提进行反驳。
采用这里提供的评估标准。
不要做没有实质内容的批判,如“这是个人观点的问题”。
对有效性的任何质疑就是对论证形式的质疑。如果某种形式的论证的前提为真而结论为假,那么这个论证是无效的,因为它有一个无效的形式。但是找到一个无效的论证并不是驳斥它的决定性理由,因为它仍然可以是一个很好的归纳论证(第6章将有更多相关讨论)。一旦一个论证被确定为有效的,逻辑思考者就应该检查它的前提是否为真,本章稍后对此进行分析。
论证评估标准(如有效性)的实用性在于:依据某一论证的前提,我们对其结论持有何种态度取决于这个论证是否符合那些标准。有效性具有这样的实际作用:当一个论证满足有效性标准时,它的形式是有效的。同时,如果我们知道这一点,我们就知道如果所有前提都为真,则结论不可能为假。因此,断言一个论证的前提而同时却否认其结论是矛盾的。例如:
例5-24 1. 如果菲利克斯是一只猫,那么它是一只猫科动物。
2. 菲利克斯是一只猫。
3. 菲利克斯是一只猫科动物。
因为论证例5-24是有效的,我们无法在不矛盾的情况下接受其前提却否认其结论。因为如果一个论证是有效的,那么如果你断言(或接受)该论证的前提,你就必须在逻辑上断言其结论。断言例5-24的前提但否认其结论就等于说了这样的话:
例5-25 如果菲利克斯是一只猫,那么它是一只猫科动物。菲利克斯是一只猫。但是,它不是一只猫科动物。
很显然,这三个语句不可能同时为真。例5-25应该被驳斥,因为三个语句是一个逻辑上不可能的集合:没有一个可能世界使得所有语句都为真。
无效性的实际作用是什么呢?答案如下:
如果你知道一个论证是无效的,你就知道它的前提可能全部为真,而同时结论却为假。
但是要注意:
如果你对一个论证唯一知道的就是它是无效的,那么你并不知道它的前提事实上为真,并且结论事实上为假。
你只是知道这样的场景是可能的:论证形式使得这种场景成为可能(在有效论证形式中不可能发生的情况)。综上所述,在无效性的所有情况下,论证都不具备保真性。因此,前提和结论的真值的任何组合在逻辑上都是可能的。
可靠性
那么,我们必须总是接受有效论证的结论吗?不是的,因为有效论证的结论仍然会存在某些错误(上述有些例子清楚地表明了这一点)。评估一个论证,有效性是我们首先使用的标准,但是并不是唯一的标准。在确定一个论证有效之后,我们还必须确定它是否可靠,记住:
一个论证是可靠的,当且仅当它是有效的,且它的所有前提都为真。
因此,再来看前面给出的一些论证:
例5-22 1. 没有伯罗奔尼撒人是埃维厄人。
2. 所有斯巴达人都是伯罗奔尼撒人。
3. 没有斯巴达人是埃维厄人。
例5-4 1. 所有狗都是鱼。
2. 所有鱼都是哺乳动物。
3. 所有狗都是哺乳动物。
例5-5 1. 所有民主党人都是素食主义者。
2. 所有素食主义者都是共和党人。
3. 所有民主党人都是共和党人。
专栏5-6 可靠的论证
(1)一个论证是可靠的当且仅当它是有效的,且它的所有前提都为真。
(2)一个论证是不可靠的,如果该论证不具备有效性或真前提,或两者都不具备。
(3)不可靠性是驳斥一个论证的理由,即使这个论证是有效的。
(4)一个可靠论证的结论是真的。
(5)根据(4),如果一个可靠论证的结论没有表述错误的事物,结论就不能被驳斥。
论证例5-22是可靠的。但是论证例5-4和例5-5是不可靠的。这是因为,如果一个论证缺少有效性或者真前提(或者缺少两者),那么它就是不可靠的。论证例5-4和例5-5的问题在于它们的前提是假的,因此使得它们不可靠,即使如我们所见,这两个论证都是有效的。有几个要点必须记住。首先,即使一个论证只有一个前提为假,这个论证也是不可靠的,无论其是否有效。其次,一个前提只有在毫无疑问为真的情况下才是真的。最后,因为有效性是可靠性的必要条件,一个论证也可能因为其形式的无效而是不可靠的。例如:
例5-26 1. 任何一个作为国家首都的城市都是一个政治权力中心。
2. 芝加哥是一个政治权力中心。
3. 芝加哥是一个国家的首都。
这里的两个前提都是真的,但是论证还是不可靠的,因为它是无效论证。
有效性和真前提是可靠性的必要条件(见图5-1)。一个论证的前提事实上是否为真又完全是另一个问题(无法仅用逻辑来回答)。大多数此类问题都是通过科学,或者历史学家、地理学家以及其他事实发现者的观察来回答的。为了确定前提是否为真,一个经验丰富的逻辑思考者希望直接了解事实!但这就使得他必须去图书馆或实验室,并且仔细考虑论证前提的证据──这些论证都被声称是可靠的。
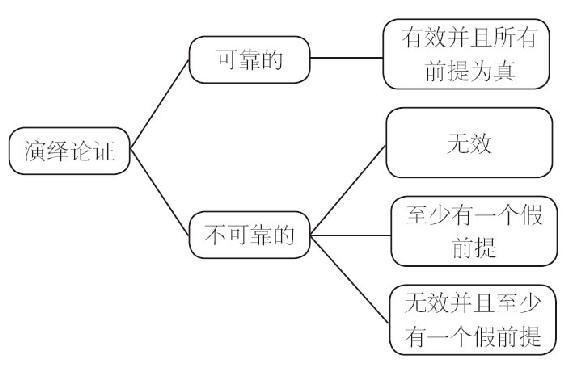
图5-1 可靠性
可靠性的实际作用
那么,为什么可靠性如此重要呢?为什么可靠性是论证必须具备的一个特征呢?因为,如果知道一个论证是可靠的,那么我们不仅完全有理由接受其结论,而且必须接受其结论!如上述定义所示,所有有效论证都是保真的:如果前提为真,则结论必定为真。如果一个论证是有效的并且前提事实上也为真,那么它就是可靠的。也就是说,前提的真值传递给了结论。因此,任何此类论证(没有论述任何错误的事物的论证)的结论都不能被驳斥。
可靠性有一个实际的影响或价值,因为只要一个演绎论证符合这个标准,那么它的结论就确保为真。事实上,可靠性的实际作用有两个方面。
如果一个论证是可靠的,那么:
在论证有效的条件下,你无法在没有矛盾的情况下断言其前提却拒绝其结论。
在论证有效并且其前提全部为真的条件下,你无法在不说错话的情况下拒绝其结论。
那么不可靠性呢?它对于逻辑思考者的实际作用是什么?一个不可靠的论证不能保证其结论的真。如果一个论证有效但不可靠,就意味着它至少有一个假前提。认识到这一点就是拒绝该论证的充分理由。如果一个论证不可靠但是所有前提都为真,就意味着其论证形式是无效的:正如我们将在第6章所看到的,有些这样的论证最好被看作归纳论证,并且用可靠性之外的标准来评估。
说服力
有效性和可靠性不是评估演绎论证的全部标准。还有一个演绎说服力的标准:如果一个论证具备专栏5-7中的三个条件,就认为该论证满足说服力标准。
专栏5-7 说服力的三个条件
(1)可识别的有效性。
(2)可接受的前提。
(3)比结论更加明确可接受的前提。
根据条件(1),一个有说服力的论证的有效性必须对评估论证的逻辑思考者是显而易见的。根据条件(2)和条件(3),一个有说服力的论证的前提应该为逻辑思考者接受论证的结论提供很好的理由。注意,这并不要求有说服力的论证是可靠的。换句话说,一个不可靠的论证也可能有说服力,只要思考者识别出论证的有效性,并且前提为结论提供了很好的理由;即使至少有一个前提是假的,而思考者对此并不知情。假设一个思考者在图书馆看到过英格里德并且进行如下推理:
例5-27 1. 英格里德在图书馆。
2. 如果英格里德在图书馆,那么她不在自助餐厅。
3. 英格里德不在自助餐厅。
因为他正好看到英格里德在图书馆,他似乎有证据支持前提(1)为真。前提(2)也是真的,因为没有人能够同时出现在两个不同的地方。根据前提(1)和前提(2),可以有效得出肯定前件式的结论3。因此这个论证是演绎有说服力的:论证具有可识别的有效性,并且有支持结论的可接受的前提。但是,假设思考者并不知道他在图书馆看到的事实上并不是英格里德本人,而是她的孪生妹妹格里塔。在这种情况下,该论证就是不可靠的──但仍然很有说服力!
另一方面,有时候可靠的论证也可能没有说服力。可识别的有效性和真前提可能并不足以使一个论证有说服力。例如:
例5-28 1. 地球不是平的并且地球不是宇宙的中心。
2. 地球不是宇宙的中心。
例5-28很显然是有效的,因为如果其前提为真,结论不可能为假。此外,因为其前提事实上确实为真,所以论证也是可靠的。但是对例5-28的结论持合理质疑的人可能不会被说服而接受它。例5-28没有满足上述的条件(3),即有一个比结论更明确可接受的前提。假设这个论证是在中世纪被提出的,所有的证据都指向结论的假。尽管因为不知道这个前提是真的──并且这个论证是可靠的,那时的人们可能就会拒绝前提1。因此,即使是可靠的论证也可能不能说服人──当论证的前提并不比它们所支持的结论更可接受的时候。
专栏5-8 本节小结
满足专栏5-7中三个条件的演绎论证的前提,为逻辑思考者接受论证的结论提供了很好的理由。
说服力的实际作用
任何识别出某个论证的有效性及其前提为结论提供良好理由的人,在理性上都不可能拒绝该论证。这样的论证可以被称为“理性上强制的”(或者简单地称为“强制的”)。如果思考者要拒绝这样的论证,那么他就是不理性的:这在逻辑上讲不通。因为论证例5-28不能说服思考者基于论证的前提接受其结论,这个论证就是无说服力的(即,不是理性上强制的)。逻辑思考者必须防范这类论证并且尽量避免它们。在第8章我们将讨论辩论过程中影响有效论证基至可靠论证的说服力的一种错误。
