我们经过研究发现,各种各样的现象都呈正态分布,就像图A–1中显示的那种钟形曲线。例如,如果我们要画图显示不同母鸡每周产蛋的数量,生产某型号汽车的过程中出现错误的数量,或者一群人的智力测试分数,代表这些数据的曲线的形状大体上都接近钟形。我们无须了解这些分布呈现钟形背后的数学原理。重要的是正态分布曲线用处很大,能够帮助我们找出一个观测值与另一个观测值之间的联系。图A–1中显示的正态分布曲线按照标准差——用“标准差”来代表平均分与平均值的偏离程度——分为几段。如果观测值的数量足够多,正态分布的曲线就无限接近钟形,也就是非常标准的正态分布。在标准的正态分布中,大约68%的观测值都分布在偏离平均值(也就是图A–1中的曲线上0的位置)+1或–1个标准差的范围内。标准差的概念还有一些用处,那就是百分位排名与标准差的关系。在所有的观测值中,大约84%的数据都集中在+1个标准差或少于+1个标准差的范围内;超出平均值+1个标准差的观测值在整个分布中对应的百分位排名就是第84位。几乎98%的观测值都集中在+2个标准差的范围内。正好超出平均值+2个标准差的观测值在整个分布中对应的百分位排名就是第98位,剩下的2%观测值对应的百分位排名则高于第98位。几乎所有的观测值都位于+3或–3个标准差的范围内。按照惯例,大多数智力测试都将智商的标准差设定为15分(平均智商设定为100分)。
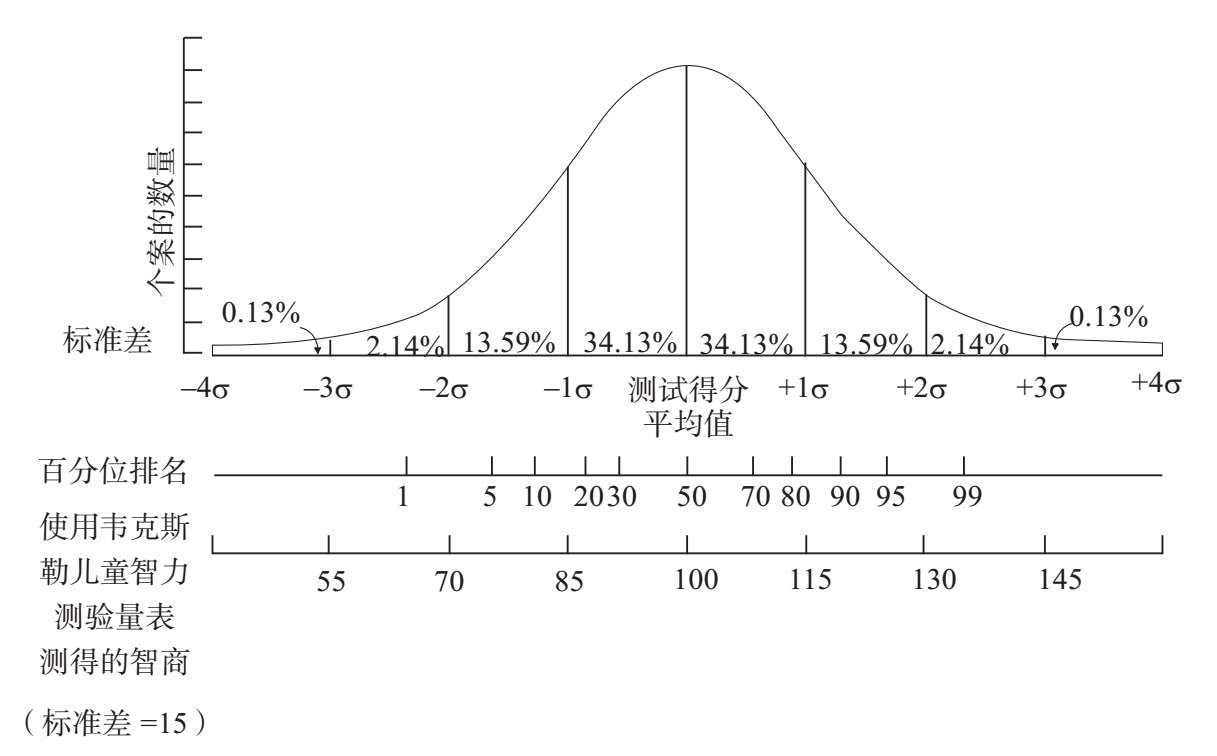
图A–1 正态分布曲线
标准差这一单位非常有用,我们可以用标准差来表示效果值的大小。例如,一项新的教学方法改善学习效果的程度就可以用标准差来表示。最常用的效果值的指标叫作Cohen’s d,是这样计算的:A组的平均值减去B组的平均值再除以A、B两组的标准差之和(或者有时候只除以A组的标准差)。
按照惯例,d的值为0.2或更小就被视为效果甚微。这相当于将实验组分数的百分位排名从第50位提高到将近第60位。如果新的教学方法(百分位排名第60位)和老的教学方法(百分位排名第50位)相比能够使孩子的成绩排名提前10名,你或许并不认为这是很小的效果。你是否愿意付钱使用新的教学方法,一部分也取决于百分位排名从第50位上升到第60位究竟具有多么重要的意义。如果你用孩子盲打的速度达到每分钟40字的熟练程度所需要的时间来衡量教学的效果,只需要几天的时间就可以将百分位排名从第50位提高到第60位,很可能你就不愿意为这样的进步花费太多的钱,也不愿意学校在上面花费太多。如果你根据SAT数学考试的平均成绩来衡量两所高中采用的数学教学方法的效果,采用一种教学方法后数学考试的平均成绩是500分,而采用另一种教学方法的平均成绩是520分,这就是百分位排名第50位与第60位之间的差距(假设SAT分数的标准差是100)。你或许愿意为了孩子的分数得到这样的提高而不惜花上大笔钱财。或许你还乐意你们的教育委员会为每位学生花上一些钱,以采取更有效的教学方法。
按照惯例,d的值为0.5左右被视为是一般的效果。不过,在智力测试和学业成就的概念里,这么大的效果值一般已经相当引人注目了,这相当于SAT数学部分的分数从500分提高到550分——有时这样的差距就是考取中上水平的大学和考取名牌大学的差距。为了使普通孩子的SAT数学成绩百分位排名从第50位提高到大约第70位(这就是0.5个标准差对应的效果值),你和学校或许愿意花大价钱采用新的教学方法。
0.7~1个标准差被认为是很大的效果。1个标准差对于教育和智力的差距来说是非常大的。一般认为黑人与白人的智商差距就接近1个标准差。在第6章中,我们讨论了黑人与白人的实际差距是否有如此之大。如果有,那就意味着黑人的平均智商在白人的智商分布上对应的百分位排名是第16位。如果一项干预措施能够使孩子在全国数学考试中的百分位排名从第50位提高到第84位,那么人们一定认为在这项干预措施上花一大笔钱是值得的。对于一个国家来说,如果数学成绩取得了这样的进步从而使国家的竞争力有所增强,那么国家就应该不惜成本地大力普及这项干预措施。
相关系数可以用来测量两个变量之间线性联系的程度。例如,智商与学习成绩之间的相关度恰好是0.5左右,也就是说两者的联系较强。不过智商与学习成绩之间至少应该具备相当的关联度,因为设计智力测试就是为了预测人们在学校内的学习成绩。相关系数的变化范围是–1到+1之间,–1表示两个变量完全成反比,+1表示两个变量完全成正比。相关系数为0就意味着两个变量之间没有任何联系。相关系数也可以用来衡量效果值的大小,或者关联度的大小。相关系数的数值小于0.3就是较小的相关度,0.3~0.5就是中等大小的相关度,在0.5以上就是较大的相关度。但是,和效果值一样,关联度是否重要取决于关联度中的变量,而不是相关度的大小。我们也可以用标准差的概念来解释相关系数。如果两个变量的相关度是0.25,那么第一个变量增加1个标准差,第二个变量就会增加0.25个标准差;如果相关度是0.5,那么第二个变量就会增加0.5个标准差。如果班级的规模与学生在标准化考试中的成绩之间的相关度是–0.25,那么班级规模缩小1个标准差,学生的考试成绩就应该提高0.25个标准差(假设班级规模与考试成绩之间确实存在因果关系)。
多元回归是一种分析方法,它能够找出一些因变量(或预测变量)与结果变量(或某个目标变量)之间的关系。例如,我们或许想要比较哪些变量能够最大限度地预测一所房子在房地产市场上的吸引力。我们可能会衡量房屋的面积有多少平方米,有几间卧室,卫生间的舒适程度(例如水池的数量、是否能洗热水澡、使用的材料质量好坏等),小区的平均收入,以及由潜在买主的数量代表的房屋的抢手程度。然后我们将这些变量同时与房屋在市场上的吸引力联系在一起,也就是房屋在市场上的售价——目标变量。不考虑所有其他变量对房屋价值的贡献度(即将所有其他变量设为常数)的条件下,找出某个变量与市场价值之间相关度的大小,就可以估计出这个变量对于房屋市场价值的贡献度。因此,当将所有其他变量设为常数时,房屋的抢手程度与市场价值之间的相关度可能是0.25,卫生间的舒适程度与市场价值之间的相关度可能是0.1。不过所有这些变量之间都存在一定的相关度,并且对某些变量的测量可能比其他变量更为准确,某些变量可能与其他一些变量存在一定的因果关系,而与另一些变量不存在因果关系,有些没有测量的变量或许会对一些得到测量的变量产生一定的影响。这就导致多元回归的结果有可能对我们产生误导。房屋的抢手程度与市场价值之间的实际相关度,可能远远高于多元回归分析得出的0.25,也可能远远低于0.25。
有无数个例子能够说明,多元回归分析得出的因果关系,往往与实验得出的因果关系不一致。从因果推论的角度来看,这些实验几乎都比多元回归分析更加可取。例如,大概在15年前,我曾经参加过全美卫生研究院召开的共识发展会议。这次会议的目的就是要重新审视关于冠状动脉阻滞的治疗方法的研究,究竟是临床治疗还是手术治疗效果更好,并就这两种治疗方法的适当性达成共识。要审查的研究中有大量研究都是由政府资助的,耗资巨大。在这些研究中,研究人员将大量和患者有关的变量放入一个多元回归方程式中,例如病史、年龄以及社会经济地位等,然后在不考虑不同患者使用的其他治疗方法的情况下,确定某种治疗方法的疗效。但是由于美国管理研究政策的内部审查委员会要求,必须给予患者选择治疗方法的自由(不过我们并不能确定这样做实际上是否真的符合患者的利益),所以所有的实验证据都因为带有自我选择的人为因素而动摇了。不过除了美国的研究以外,还有两项欧洲的研究,都达到了随机为患者安排各种治疗方法的标准。因此,专门小组的成员放弃了耗资巨大的美国研究,只对两项欧洲研究的结果进行了分析。
让我们再考虑一个与本书更为相关的例子,那就是班级规模是否真的会影响学习成绩。多元回归分析告诉我们,不考虑学校的规模、学校所在社区全部家庭的平均收入、教师的薪酬、具备资格的教师的比例,以及学区内每名学生的教育支出等因素,规模一般的班级与学生的学习成绩之间没有联系。在另外一项随机选取研究对象并实施得很好的研究中,进行比较的班级学生人数相差很多(将有13~17名学生的班级与有22~25名学生的班级进行比较)。结果这项研究发现,将班级人数缩减至13~17人,学生们在标准化考试中的成绩提高了0.25个标准差以上——这对黑人孩子起到的作用也大于白人孩子(1999年)。这不仅仅是另外一项有关班级规模的影响的研究,它还取代了所有有关班级规模的多元回归研究。
在本书中我偶尔会提到多元回归研究,不过每次都会提醒大家注意研究的结果。
自我选择是相关性研究和多元回归分析面临的难题之一。有很多原因要求我们必须要对自我选择有所了解。如果我们说智力与未来的职业成就之间具有一定的相关度——比如0.4,那么大家往往就会条件反射地认为,这样的关系完全是因果关系——智商更高的人工作能力也更强。但是智力与其他因素也是相关的,例如智商较高的孩子通常其父母的社会经济地位也较高。如果父母的社会经济地位较高,那么不论这个孩子智商高低,都更有可能念大学。同样,不论这个孩子的智商高低,拥有大学学历就有可能获得更高的职业地位。因此,智力与职业成就之间的关联就受到了其他因素的影响,例如父母的社会经济地位以及大学学历,那么这个孩子,或是研究的对象,就具备了“自我选择”的自由。(说一个人“自我选择”了父母的社会经济地位恐怕并不恰当,因为显然这是不可能的。但是由于真正进行比较的研究人员不能决定这个变量的大小,所以就好像是研究对象决定了这个变量的大小。总之,一些与研究对象有关的变量是研究人员无法控制的,其大小也不能由他们选择,有时他们甚至不知道这些变量的变化。)
只要一项研究仅对一个特定的变量进行测量而不是控制,我们就一定要注意到,对测量的变量(以及所有其他测量或不测量的变量)的大小进行选择的是研究对象,而不是研究人员。这就在很大程度上限制了推理的准确性。在班级规模的例子中,研究人员使用了多元回归的方法,使得班级规模这个变量的大小可以进行自我选择(也就是说,研究人员不决定班级规模的大小),并且班级规模这个变量也许与其他各类变量都有联系,这些变量有可能会扩大或限制班级规模对于学习成绩的影响。能够完全避免自我选择问题的唯一方法,就是让研究人员来选择因变量或预测变量的大小(例如,是人数较多的班级还是人数较少的班级),然后观察因变量或预测变量对目标变量的效果(例如成就测试的成绩)。由于不是总能做到这一点,所以我们只好满足于相关性分析和多元回归分析,同时对自我选择的问题保持警戒。
最后,统计显著性告诉我们,如果一项计划实际上并没有任何效果,那么研究得出的效果值——例如班级规模对于学习成绩的效果——就有可能是偶然产生的。按照惯例,如果统计显著性的值为0.05,这就是说,在与进行的研究设计相同的研究中,两个平均数之间的差距或某个特定大小的相关度在100次统计中只有5次出现的概率,或者20次中只有一次出现的概率。不过统计显著性在很大程度上取决于观测值的数量。如果观测值数量足够多,那么即使在实践中或理论上小到不具备任何意义的差距,在统计学上也可能会很重要。我在本书中提到的任何一项研究所得出的结果,其统计显著性都达到了低于0.05的水平。只有一项我称为“不太重要”的研究结果,其发生的概率低于0.1,这项研究的结果有可能是偶然获得的。
