埃涅阿克计算机配备了18000个真空管,重30吨;未来的计算机可能只有100个真空管,质量约为1.5吨。
——大众机械,1949年
计算机科学的研究范畴不仅仅是电脑,就像天文学的研究范畴不仅仅是望远镜。
——E.W.Dijkstra
在进一步思考奇点的含义前,让我们先研究各种服从于加速回报定律相关技术的广阔领域。摩尔定律是最著名的(也是被广为承认的)指数增长现象。在20世纪70年代中期,戈登·摩尔(集成电路的主要发明人、英特尔公司的董事长)指出,我们可以每24个月在集成电路上集成现在两倍的晶体管(在20世纪60年代中期,他曾预计12个月)。电子的传导距离随着减少,电路也将运行得更快,从而提高了整体计算能力。这些带来的结果是计算的性价比以指数增长,其翻倍的速度(12个月翻一番)远快于范式迁移的增长速度(10年翻一番)。信息技术在性价比、带宽、容量等方面的速度增长1倍的时间都是一年。
摩尔定律的主要动力是半导体元件尺寸的减少,减少的速度为每5.4年收缩一半(见图2-6)。由于芯片功能是双向的,这意味着每2.7年每平方毫米的元件数量将增加一倍22。
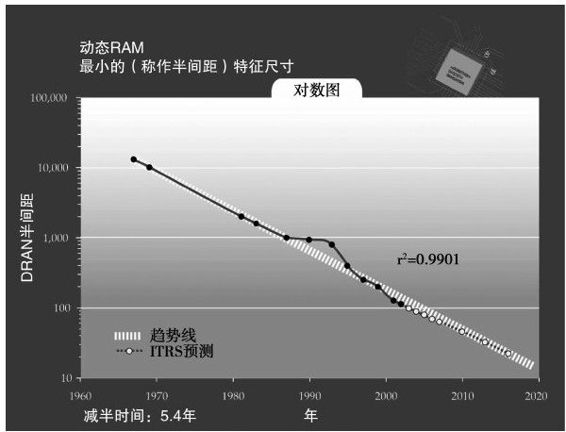
图 2-6
图2-6展示了半导体工业发展路线图(选自半导体技术协会的国际半导体技术蓝图《参考系》,该图预测至2018年)。
每平方毫米DRAM(动态随机存取记忆体)的成本也已开始下降。每1美元生产DRAM比特数的倍增时间只需1.5年23(见图2-7)。
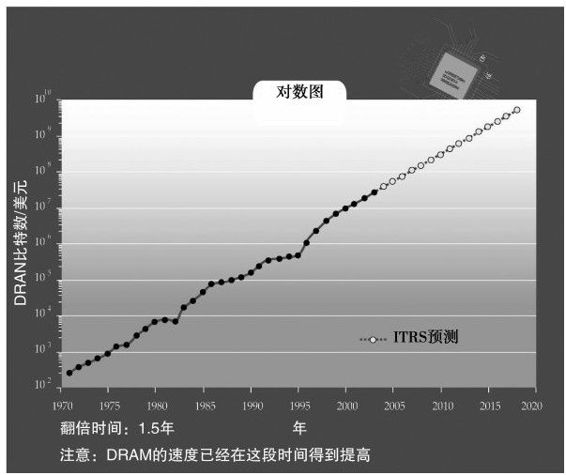
图 2-7
晶体管方面也可以看到类似的趋势。1968年1美元可购买1个晶体管;2002年1美元可以购买大约1000万个晶体管。由于DRAM是一种专门的领域(有自己的创新),晶体管的平均价格减半的时间略长于DRAM,约1.6年(如图2-8)24。

图 2-8
半导体性价比显著而平稳的加速,是通过改良生产过程中不同阶段、不同方面的工艺技术实现的。关键元件尺寸已小于100纳米(通常认为100纳米是应用纳米技术的极限)25。
与格特鲁德·斯坦因诗中的“玫瑰”不同,“晶体管是晶体管是晶体管”并不适用于现实情形。事实上,晶体管不是一成不变的,在过去30年中,它们已经变得体积更小、价格更便宜、速度更快了(参见图2-10)——因为电子的传输路程更短了26。
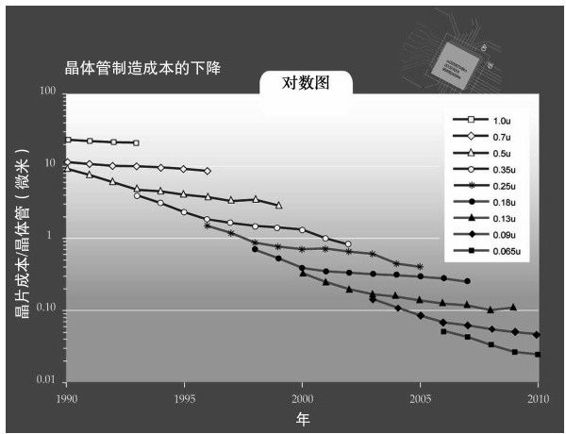
图 2-9
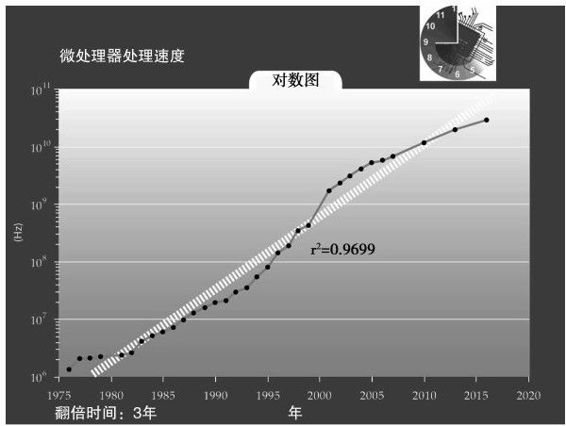
图 2-10
如果把晶体管成本的下降和晶体管间延时减少的趋势结合起来,我们会发现,只需要1.1年的时间晶体管周期的单位成本就会减半(见图2-11)27。晶体管周期的单位成本是一个能够准确地从整体上衡量性价比的指标,因为这个指标可以同时考虑到速度和容量。但是晶体管周期的单位成本没有考虑更高层次的技术革新(比如微处理器的设计)对计算性能的改进。
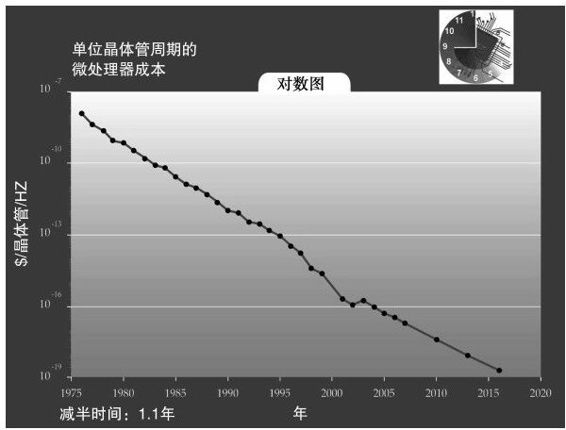
图 2-11
英特尔处理器中的晶体管数量每两年翻一番(见图2-12)。还有一些其他的因素也在改进整体性价比,比如时钟速度的提升、微处理器成本的下降以及处理器设计方法的创新28。

图 2-12
处理器的MIPS(每秒的指令执行数目)性能,每1.8年提升一倍(见图2-13)。而且,在这段时间内处理器的单位成本也在下降29。
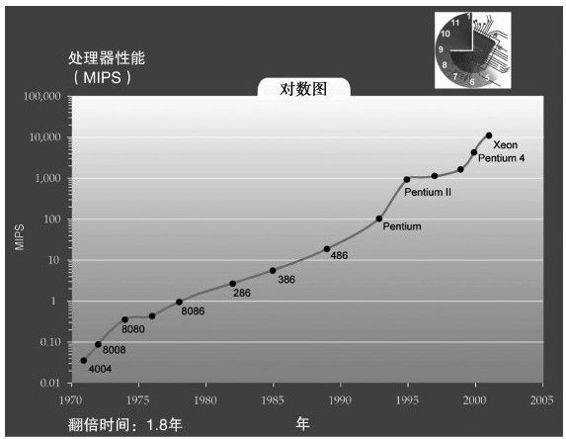
图 2-13
让我来回顾这40多年来对计算机产业的切身体会,比较一下我在学生时期(1960年前后)使用的MIT计算机和现在的笔记本电脑:1967年,我曾经使用过价值数百万美元的IBM 7094计算机,32K字节(36bit)的内存储器,处理器速度为1/4 MIPS。2004年,我使用的是一台价值2000美元的个人电脑,几个G的RAM,处理器速度为2000MIPS。MIT计算机的价格大约是个人电脑的一千倍左右,所以现在个人电脑的MIPS的单位成本是MIT计算机的800万分之一,如表2-1所示。
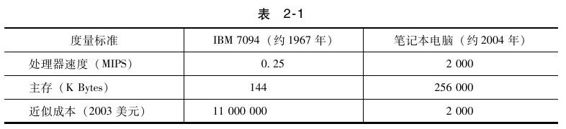
现在我的计算机处理器的能力达到了2000MIPS,其处理成本不到1967年我使用的计算机的224分之一,也就是说性价比在37年间翻了24番,大约每18.5个月翻一番。相比之下,2004年我使用的计算机RAM的容量增长了近2000倍、磁盘存储大幅度增长、指令集也更高效。此外通信速度更快,软件功能更强,其他方面的性能也不断得到提升,所以在未来性能翻倍的时间将会越来越短。
尽管信息技术的成本大幅度降低,但需求增长的速度更快。比特的数量每1.1年翻一倍,比单位比特成本降低一半的时间(单位比特成本降低一半大约是1.5年30)要快。半导体工业从1958年到2002年31,每年增长18个百分点。整个IT产业在GDP中的比重从1977年的4.2%,上升到了1998年32的8.2%,如图2-14所示。IT产业已经逐渐成为各种经济因素中的一股强大势力。同时IT产业也促进了很多其他制造业和服务业的快速发展,甚至包括生产桌椅板凳的制造业。各行各业的生产过程中计算机辅助设计、库存管理系统以及自动化生产系统等都得到广泛使用。
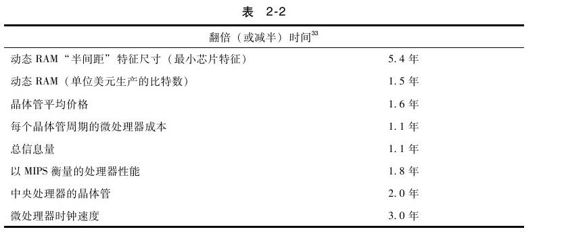

图 2-14
摩尔定律:自我满足的预言?
许多观察家都认为摩尔定律是一条已经应验的预言:工业生产商期待在未来某个特定的时间组织相应的研发。这个产业的发展路线图是典型的实例34。但是信息技术发展的指数趋势已经远远超出了摩尔定律的范畴。我们可以看到类似的发展趋势发生在每一个与信息技术相关的技术中。其中部分技术的性价比加速提高可能并不存在或者并不明显(具体解释见下文)。即便是计算本身,其性能增长的单位成本也已经远远超出了摩尔定律的预测。
第五范式35
摩尔定律实际上并不是计算机系统领域的第一阶段。如果关注性价比(1000美元的成本创造的每秒钟执行的指令数),可以在下面49个著名的计算系统和20世纪计算机相关领域中发现这个阶段(见图2-15)。
图2-15表明,当集成电路发明之前,计算性价比以指数级的速度增长就有四个不同的范式——机电、继电器、真空管、离散晶体管。摩尔范式也并不是最后的范式。当摩尔定律到达的S形曲线末端(预计2020年前)后,三维分子计算将继续推动指数级的增长,这也将构成第六范式。
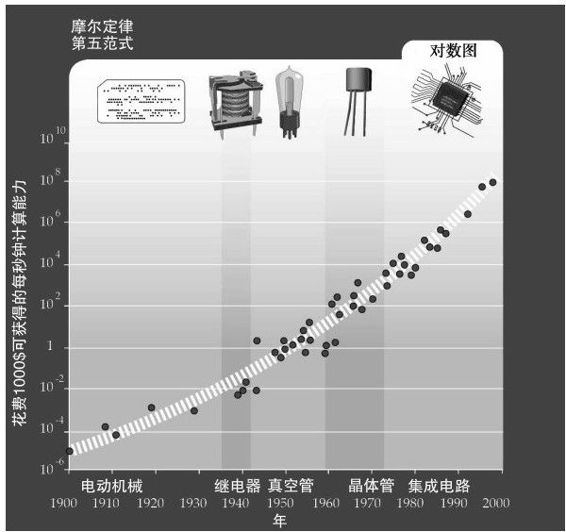
图 2-15
分形维度和大脑
注意,计算机系统第三维度的使用不是一个非此即彼的选择,而是二维和三维间的一种延续。在生物智能方面,人类大脑皮层相当的平,6个薄层被精巧地折叠在一起,这种结构可以大大增大其表面积。这种折叠的方式也可以使用第三维度。在“分形”系统(绘图更换或折叠规则迭代应用的系统)中,这种精密的折叠结构被认为构成了一部分的维度。从这一角度看,人类大脑皮层表面是一个错综复杂的二至三维结构。其他脑结构(如小脑)是三维的,但包含重复的结构,所以其本质上还是二维的。很可能我们未来的计算机系统将融合高度折叠的二维系统和充分的三维结构。
请注意,图2-15显示的是对数指数曲线,表明了两个层次的指数增长36。换言之,指数增长以指数增长的速度平稳无误地增长(对数图中的直线部分说明了指数增长;上扬的曲线显示其并不是简单的指数级的增长)。如图2-16所见,计算机的性价比在20世纪初翻一番需要三年的时间;20世纪中期翻一番需要两年的时间,而现在大约只需要一年的时间37。
汉斯·莫拉维克提供了类似的图表(见图2-16),它使用了一组不同的但是重叠的时间集合,描述计算机在不同时期(斜率的改变点)的发展趋势。从该图可以看出,斜率随着时间递进而增加,反映了指数增长的第二个层次38。
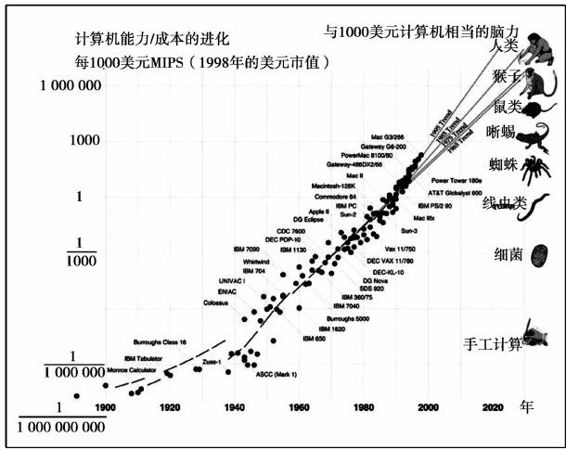
图 2-16
如果由此来预测22世纪的计算机性能发展趋势,我们可以从图2-17中看到,超级计算机将在2010年前后达到与人类大脑相当的计算性能,在2020年前后,个人电脑的计算能力将媲美甚至超越人脑的水平。这仅是我们对人脑容量的保守估计(我们将在第3章讨论关于人脑运算速度的预测)39。

图 2-17
计算机指数发展是整个科技指数化发展的一个最典型的例子。我们可以从加速度增长的角度观察指数发展的趋势:我们用了90年的时间才达到第一个MIPS/千美元,而现在我们增加1个MIPS/千美元只需要5个小时40。
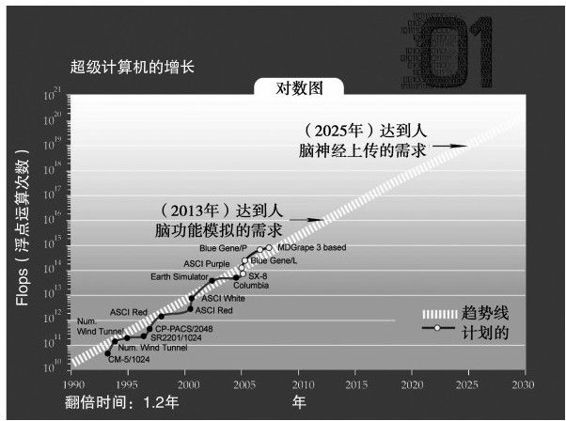
图 2-18
IBM的蓝色基因/P超级计算机,预计计算能力达到100万千兆浮点运算(每秒10亿次浮点运算),或者说到2007年41达到每秒1015次的计算能力。这已经达到了人脑计算能力的1/10——预计人脑的计算能力为每秒10 16次计算(见第3章)。如果从这个指数曲线进行推断,计算机可以在下一个10年的初期达到每秒1016计算能力。
如上所述,摩尔定律只是局限地指出了晶体管的数量在确定尺寸的集成电路中的变化,有的时候甚至还只局限在晶体管的特征尺寸变化上。最适当的性价比测量标准是单位成本的计算速度,索引可以解释不同层面的“聪明”(创新或者称为技术的演变)。除了涉及集成电路的所有发明外,计算机设计的多个层次都有改进(例如流水线、并行处理、先行指令、指导和内存缓存等)。
人类大脑使用效率很低的电化学和数字控制来模拟计算过程。其中大量的计算都是在神经元间、以200次/秒的计算速度(在每个连接)展开的。这至少比现代的电路慢100万倍。但是大脑可以从三维的、极大并行化的组织中得到巨大的能量。有许多的wings方面的技术,通过该技术可以在三维上构建电路,我将在第3章讨论。
有人也许会问:支持计算过程的物质和能量是否存在固有的限制呢?这是一个重要的问题,但正如本书第3章论述的,直到21世纪末,我们都不会接近这些限制。重要的是要区分S形曲线(以具体的技术范式为典型特征)和持续指数级增长(以一个更广泛科技领域中的持续进化过程为典型特征)。具体的范例(如摩尔定律)最终将不会保持指数增长。但是,计算的增长将最终超越它构建的范式,始终保持指数增长的速度。
根据加速回归定律,范式迁移(也称为创新)可以将任何特定模式的S形曲线转变为持续的指数增长。当旧的范式接近它的内在极限时,一个新范式(如三维电路)将接替旧的模式,这种情形在计算的历史中已经发生了至少四次。例如类人猿,每个动物掌握工具制造和使用技巧都以S形学习曲线为特征,但曲线的末端会迅速停止;与之相反,人造技术从一开始,便以指数模式迅速增长,而且永不停止。
